PVE相同品级的装备中 选择破防还是双会

95新版本以来，听说会心不再是收益最大的属性了，刚开始需要无脑对破防;现在大家装分普遍都是1w6+、1w7+，开始听说不要堆破防了，要提升会心了，破防维持在40-45左右就差不多了。

我听周边朋友说的都是以上这些定性的话，内容也比较模糊，我在网上查了下，也没有查到比较详细的定量计算。那到底当前版本多少破防是最优的呢?在现有的装备下，如何分配破防和会心收益最高呢?于是我试着自己来算算。希望能验证一下自己听到的一些结论，或者得到一些更多的信息。

先说下我搜集到的初始条件：

(1)人物属性换算：

1%破防=36.16破防等级

1%会心=41.44会心等级

1%会效=15.06会效等级

1%命中=34.2命中等级

1%无双=25.6无双等级

(2)零装分人物属性起始点：会心0.39，会效175.4，破防等级85

(3)装备属性(暂时不考虑精简，仅考虑破防or双会+命中or无双的普通装备)：

破防等级+会心等级+会效等级=装分*0.1151-加速等级

会心等级：会效等级=2.18

(4)伤害公式：

伤害=技能伤害*(1+破防)*(会心*(会效-1)+1-偏离-识破*0.75)

根据伤害公式，可以定义收益系数Y=(1+破防)*(会心*(会效-1)+1-偏离-识破*0.75)。伤害=技能伤害*收益系数Y

接下来就继续看看收益系数Y与破防、会心这些属性的关系。

先定义一下：

Y=收益系数

a=破防

b=会心

c=会效

d=命中

e=无双

M=总装分

boss满命中A：

boss识破B：

目前的装分，除了命中和无双有可能溢出外，相信没人会会心溢出，那么根据圆桌理论：

Y=(1+破防)*(会心*(会效-1)+1-偏离-识破*0.75)

=(1+a)*(b*(c-1)+1-(A-d)-(B-e)*0.75)

根据之前提到的装备属性(暂时不考虑精简，仅考虑破防or双会+命中or无双的普通装备)：

破防等级+会心等级+会效等级=装分*0.1151-加速等级

会心等级：会效等级=2.18

可得：

b=(0.1151*M-(a*36.16-85))/3.18*2.18/41.44/100+0.0039

c=(0.1151*M-(a*36.16-85))/3.18/15.06/100+1.754

将b和c带入，

Y=(1+a)*(b/100*(c-1)+1-(A-d/100)-(B-e/100)*0.75)

=(1+a)*(((0.1151*M-(a*36.16-85))/3.18*2.18/41.44/100+0.0039)/100*(((0.1151*M-(a*36.16-85))/3.18/15.06/100+1.754)-1)+1-(A-d/100)-(B-e/100)*0.75)

=f(a)

于是我们可以得到一个以破防为变量的收益函数：Y= f(a)

好了，咱们暂停一下，先不忙说这个Y= f(a)。

咱们先说说这里面的总装分M的实际意义。

在游戏中我们人物的总装分一般都1w6+或者1w7+，这个总装分对应着我们的各个属性。之前谈到了普通装备的装分和属性的规律：破防等级+会心等级+会效等级=装分*0.1151-加速等级。除了这些普通装备外，还有附魔、五行石、五彩石、小药、阵等等各种收益。如果将这些收益除去，那么剩下的装分和人物属性就应该满足破防等级+会心等级+会效等级=装分*0.1151-加速等级。

那么反过来想，如果我身上没有附魔、五行石、五彩石、小药、阵等等各种收益，只穿普通装备，需要多少装分才能达到我目前的人物属性呢，这个装分，我姑且叫他当量装分，意思就是为了达到你目前的人物属性，需要穿多少装分的普通装备才能达到。

根据之前的描述，当量装分=(a*36.16-85+(b-0.39) *41.44+(B47-175.4%)*15.06)/0.1151

那么回到刚才的收益函数Y= f(a)，如果希望这个函数能体现附魔、五行石、五彩石、小药、阵等等各种收益，那么其中的总装分M就应该是当量装分而不是你游戏里实际的装分。

当然，我承认为了包含附魔、五行石、五彩石、小药、阵等等各种收益，我提出当量装分这个概念可能不妥，这也是我目前能想到的一个简化处理的方式。当然，由于各种收益的各个属性之间的比例和普通装备的属性是有一定偏差(比如得到的会心收益比会效收益就不一定等于2.18)，会造成收益函数会有些偏移，抱歉。

好，咱们继续聊这个收益函数：Y= f(a)。

根据之前的描述，

Y=f(a)=(1+a)*(((0.1151*M-(a*36.16-85))/3.18*2.18/41.44/100+0.0039)/100*(((0.1151*M-(a*36.16-85))/3.18/15.06/100+1.754)-1)+1-(A-d/100)-(B-e/100)*0.75)

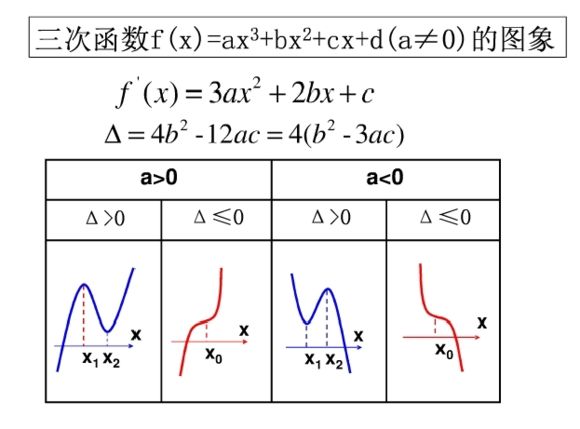
这是一个关于a的三次函数。三次函数的图像是什么还记得吗?

看到了么，不同的常数项会造成三次函数的不同曲线。在第一种和第三种曲线中，是会出现局部最高值的。这意味着，收益函数Y= f(a)在a∈(a1,a2)中，有可能会出现某个值a，对应着这段函数的最高值。

于是我将自己目前的属性输入

Y=f(a)=(1+a)*(((0.1151*M-(a*36.16-85))/3.18*2.18/41.44/100+0.0039)/100*(((0.1151*M-(a*36.16-85))/3.18/15.06/100+1.754)-1)+1-(A-d/100)-(B-e/100)*0.75)

我的属性是：破防46%，会心17%，会效190%，命中105%，无双22%，实际装分17200，经计算当量装分21603,

然后假设我的输出对象是97木桩，满命中105%，识破25%

将以上常量代入：Y=f(a)，该函数在破防20%-80%区间的函数图像如下：

从该曲线得出，收益系数是随着破防比例而递增的，也就是说，破防越高，收益系数Y越大。这也印证了网上朋友所说的，95版本初期破防的收益最高这个结论。那么回到这个帖子的标题，意思就是说，相同品级的装备，选择破防or双会?现在我可以比较放心的说，以我现在的装分，应该选择破防。

还有朋友说，等以后装分提升了，总属性增加了，破防的收益会渐渐不如会心。可是这也是个模糊的概念，到底装分提高到多少就不再无脑堆破防了呢?这个时候，破防应该是多少才是最优的呢?

我尝试输入：破防50%，会心25%，会效220%，命中105%，无双22%

得到以下曲线：

从这个曲线得到，在当前属性下，并不是破防越高越好，收益系数最大值出现在破防45%左右的地方，那么对于我“破防50%，会心25%，会效220%，命中105%，无双22%”的这个假设属性，适当将一些破防装备换成双会的，将破防压在45%左右，收益更高。

再大胆一些，到了版本后期，假设：破防40%，会心60%，会效230%，命中105%，无双25%

从这个曲线可以看到，当总属性已经比较高的时候，破防再提升，收益系数的衰减就比较厉害了，此时应该优先堆会心了，破防压在40%左右，总收益系数最高。当然，到了后期，属性膨胀，还需要考虑会心溢出的问题了。

为了方便查询自己当前状态的最佳破防值，我制作了一个excel表格，输入自己当前的各个属性(破防，会心，会效，命中，无双)，再输入输出对象的属性(满命中，识破)，能自动计算生成Y=f(a)曲线，自己通过曲线就可以查到在自己当前装分下，破防是否是最佳值。

稍后我会将这个excel表格上传，供大家参考。

好了，这个帖子的标题是【相同品级的装备，选择破防or双会】，这个问题大致说完了。

不过，我看看这个收益系数Y=(1+破防)*(会心*(会效-1)+1-偏离-识破*0.75)

=(1+a)*(b*(c-1)+1-(A-d)-(B-e)*0.75)

想着让它再发挥点余热。